Mk2 and Mk-n Models of character evolution
make.mkn.RdPrepare to run a Mk2/Mk-n model on a phylogenetic tree and
binary/discrete trait data. This fits the Pagel 1994 model,
duplicating the ace function in ape. Differences with that
function include (1) alternative root treatments are possible, (2)
easier to tweak parameter combinations through
constrain, and (3) run both MCMC and MLE fits to
parameters. Rather than exponentiate the Q matrix, this
implementation solves the ODEs that this matrix defines. This may or
may not be robust on trees leading to low probabilities.
Arguments
- tree
An ultrametric bifurcating phylogenetic tree, in
ape“phylo” format.- states
A vector of character states, each of which must be 0 or 1 for
make.mk2or 1 tokformake.mkn.- k
Number of states to model.
- strict
The
statesvector is always checked to make sure that the values are integers on0:1(mk2) or1:k(mkn). IfstrictisTRUE(the default), then the additional check is made that every state is present. The likelihood models tend to be poorly behaved where states are missing, but there are cases (missing intermediate states for meristic characters) where allowing such models may be useful.- control
List of control parameters for the ODE solver. See Details below.
Details
make.mk2 and make.mkn return functions of class mkn.
These functions have argument list (and default values)
f(pars, pars, prior=NULL, root=ROOT.OBS, root.p=NULL, fail.value=NULL)
The arguments are interpreted as
parsFormake.mk2, a vector of two parameters, in the orderq01,q10. Formake.mkn, a vector ofk(k-1)parameters, in the orderq12,q13,...q1k, q21,q23,...,q2k,...qk(k-1), corresponding to the off-diagonal elements of theQmatrix in row order. The order of parameters can be seen by runningargnames(f).prior: a valid prior. Seemake.priorfor more information.root: Behaviour at the root (see Maddison et al. 2007, FitzJohn et al. 2009). The possible options areROOT.FLAT: A flat prior, weighting all variables equally.ROOT.EQUI: Use the equilibrium distribution of the model (not yet implemented).ROOT.OBS: Weight \(D_0\) and \(D_1\) by their relative probability of observing the data, following FitzJohn et al. 2009: $$D = \sum_i D_i \frac{D_i}{\sum_j D_j}$$ROOT.GIVEN: Root will be in state i with probabilityroot.p[i].ROOT.BOTH: Don't do anything at the root, and return both values. (Note that this will not give you a likelihood for use with ML or MCMC functions!).
root.p: Vector of probabilities/weights to use whenROOT.GIVENis specified. Must be of lengthk(2 formake.mk2).intermediates: Add intermediates to the returned value as attributes. Currently undocumented.
With more than 9 states, qij can be ambiguous (e.g. is q113 1->13 or 11->3?). To avoid this, the numbers are zero padded (so that the above would be q0113 or q1103 for 1->13 and 11->3 respectively). It might be easier to rename the arguments in practice though.
The control argument controls how the calculations will be
carried out. It is a list, which may contain elements in
make.bisse. In addition, the list element method
may be present, which selects between three different ways of
computing the likelihood:
method="exp": Uses a matrix exponentiation approach, where all transition probabilities are computed (i.e., for a rate matrix \(Q\) and time interval \(t\), it computes \(P = exp(Qt)\)).method="mk2": As forexp, but for 2 states only. Faster, direct, calculations are available here, rather than numerically computing the exponentiation.method="ode": Uses an ODE-based approach to compute only the \(k\) variables over time, rather than the \(k^2\) transition probabilities in theexpapproach. This will be much more efficient whenkis large.
See also
constrain for making submodels, find.mle
for ML parameter estimation, mcmc for MCMC integration,
and make.bisse for state-dependent birth-death models.
Examples
## Simulate a tree and character distribution. This is on a birth-death
## tree, with high rates of character evolution and an asymmetry in the
## character transition rates.
pars <- c(.1, .1, .03, .03, .1, .2)
set.seed(3)
phy <- trees(pars, "bisse", max.taxa=25, max.t=Inf, x0=0)[[1]]
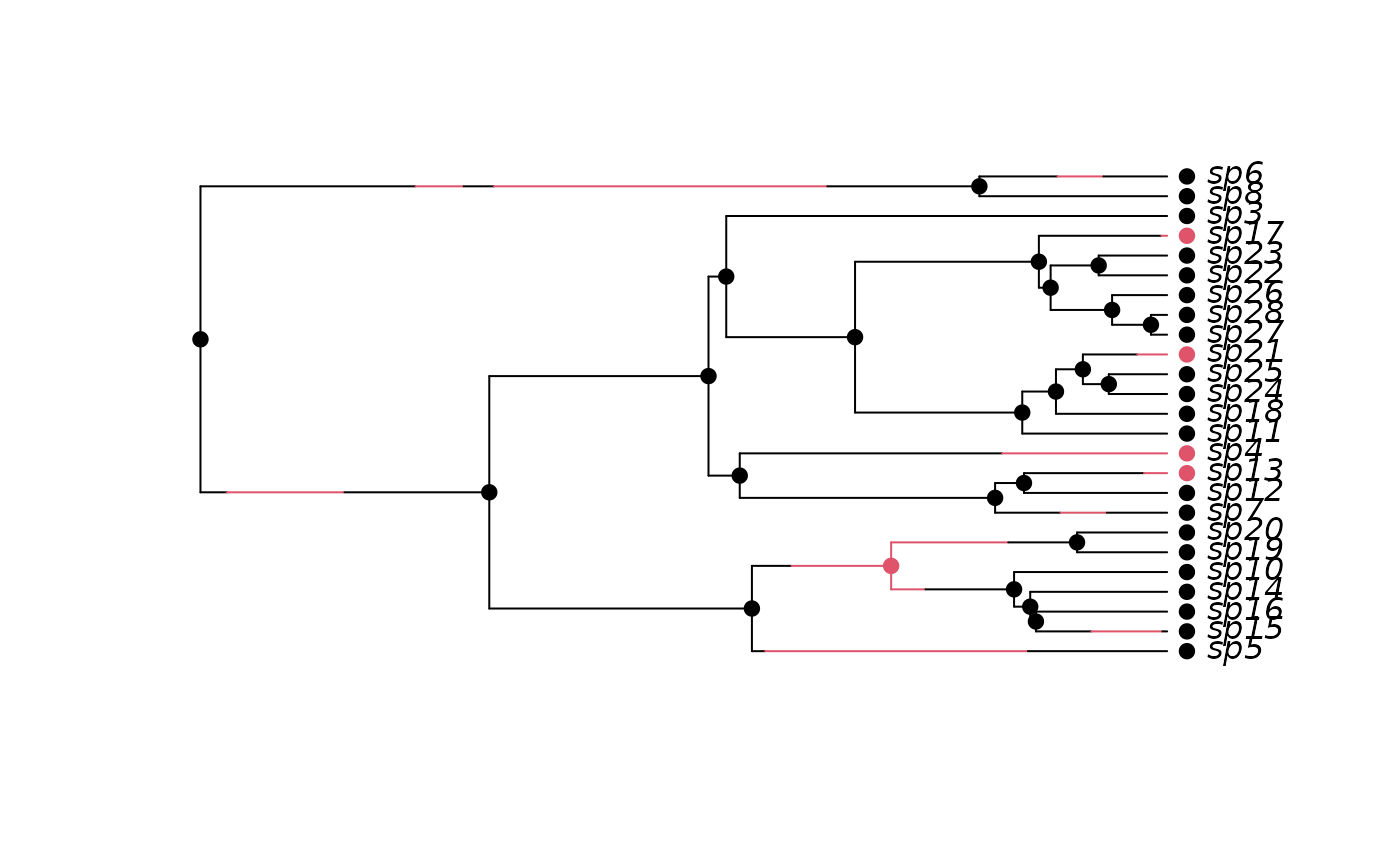
## Here is the 25 species tree with the true character history coded.
## Red is state '1', which has twice the character transition rate of
## black (state '0').
h <- history.from.sim.discrete(phy, 0:1)
plot(h, phy)
 ## Maximum likelihood parameter estimation:
p <- c(.1, .1) # initial parameter guess
if (FALSE) { # \dontrun{
lik <- make.mk2(phy, phy$tip.state)
fit.mk2 <- find.mle(lik, p)
coef(fit.mk2) # q10 >> q01
logLik(fit.mk2) # -10.9057
## This can also be done using the more general Mk-n.
## This uses an approximation for the likelihood calculations. make.mkn
## assumes that states are numbered 1, 2, ..., k, so 1 needs to be added
## to the states returned by trees.
lik.mkn <- make.mkn(phy, phy$tip.state + 1, 2)
fit.mkn <- find.mle(lik.mkn, p)
fit.mkn[1:2]
## These are the same (except for the naming of arguments)
all.equal(fit.mkn[-7], fit.mk2[-7], check.attr=FALSE, tolerance=1e-7)
## Equivalence to ape's ace function:
model <- matrix(c(0, 2, 1, 0), 2)
fit.ape <- ace(phy$tip.state, phy, "discrete", model=model, ip=p)
## To do the comparison, we need to rerun the diversitree version with
## the same root conditions as ape.
fit.mk2 <- find.mle(lik, p, root=ROOT.GIVEN, root.p=c(1,1))
## These are the same to a reasonable degree of accuracy, too (the
## matrix exponentiation is slightly less accurate than the ODE
## solving approach. The make.mk2 version is exact)
all.equal(fit.ape[c("rates", "loglik")], fit.mk2[1:2],
check.attributes=FALSE, tolerance=1e-4)
## The ODE calculation method may be useful when there are a large
## number of possible states (say, over 20).
lik.ode <- make.mkn(phy, phy$tip.state + 1, 2,
control=list(method="ode"))
fit.ode <- find.mle(lik.ode, p)
fit.ode[1:2]
all.equal(fit.ode[-7], fit.mkn[-7], tolerance=1e-7)
} # }
## Maximum likelihood parameter estimation:
p <- c(.1, .1) # initial parameter guess
if (FALSE) { # \dontrun{
lik <- make.mk2(phy, phy$tip.state)
fit.mk2 <- find.mle(lik, p)
coef(fit.mk2) # q10 >> q01
logLik(fit.mk2) # -10.9057
## This can also be done using the more general Mk-n.
## This uses an approximation for the likelihood calculations. make.mkn
## assumes that states are numbered 1, 2, ..., k, so 1 needs to be added
## to the states returned by trees.
lik.mkn <- make.mkn(phy, phy$tip.state + 1, 2)
fit.mkn <- find.mle(lik.mkn, p)
fit.mkn[1:2]
## These are the same (except for the naming of arguments)
all.equal(fit.mkn[-7], fit.mk2[-7], check.attr=FALSE, tolerance=1e-7)
## Equivalence to ape's ace function:
model <- matrix(c(0, 2, 1, 0), 2)
fit.ape <- ace(phy$tip.state, phy, "discrete", model=model, ip=p)
## To do the comparison, we need to rerun the diversitree version with
## the same root conditions as ape.
fit.mk2 <- find.mle(lik, p, root=ROOT.GIVEN, root.p=c(1,1))
## These are the same to a reasonable degree of accuracy, too (the
## matrix exponentiation is slightly less accurate than the ODE
## solving approach. The make.mk2 version is exact)
all.equal(fit.ape[c("rates", "loglik")], fit.mk2[1:2],
check.attributes=FALSE, tolerance=1e-4)
## The ODE calculation method may be useful when there are a large
## number of possible states (say, over 20).
lik.ode <- make.mkn(phy, phy$tip.state + 1, 2,
control=list(method="ode"))
fit.ode <- find.mle(lik.ode, p)
fit.ode[1:2]
all.equal(fit.ode[-7], fit.mkn[-7], tolerance=1e-7)
} # }